Accueil du site > Séminaires > Probabilités Statistiques et réseaux de neurones > Propriétés des trajectoires de la solution de l’équation des ondes stochastique en dimension spatiale 3
Vendredi 30 janvier 2004 à 10h
Propriétés des trajectoires de la solution de l’équation des ondes stochastique en dimension spatiale 3
Marta Sanz-Solé (Université de Barcelone)
Résumé : Nous étudions la continuité Höldérienne conjointe en temps et en espace de la solution de l’équation aux dérivées partielles stochastique
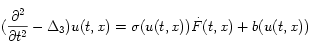
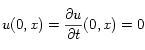
où ![]() ;
; ![]() désigne le Laplacien sur
désigne le Laplacien sur ![]() et
et ![]() est un bruit Gaussien blanc en temps et corrélé en espace.
est un bruit Gaussien blanc en temps et corrélé en espace.
Nous considérons le cas d’une corrélation spatiale de la forme ![]() ,
, ![]() et montrons que la solution de (1) est Höldérienne d’ordre
et montrons que la solution de (1) est Höldérienne d’ordre ![]() en
en ![]() , uniformément en
, uniformément en ![]() , avec
, avec 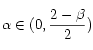 et est Höldérienne d’ordre
et est Höldérienne d’ordre ![]() en
en ![]() , uniformément en
, uniformément en ![]() , avec
, avec 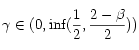 . Nous discuterons également quelques extensions à des équations non stationnaires.
. Nous discuterons également quelques extensions à des équations non stationnaires.
Dans la même rubrique :
- Jan 15 2010, 11h00 : Validation de processus ponctuels marqués de Gibbs à travers l’analyse des résidus. , Jean-François Coeurjolly (Université P. Mendes-France, Grenoble)
- Jan 08 2010, 11h00 : Classification de variables qualitatives autour de variables latentes. , Vanessa Kuentz (Universités Bordeaux 1 et 2)
- Dec 18 2009, 11h00 : Formule de représentation pour les EDSR dirigées par une martingale continue et application en Finance. , Anthony Reveillac (Université Humboldt, Allemagne)
- Dec 04 2009, 11h00 : Estimation et sélection en classification semi-supervisée , Vincent Vandewalle (Université Lille 1-Lille 2)
- Nov 27 2009, 11h00 : Equation de la chaleur stochastique avec un bruit fractionnaire de dimension infinie , Raluca Balan (Université d’Ottawa)
- Nov 20 2009, 11h00 : Apprentissage supervisé pour le diagnostic du paludisme à haut-débit : réconcilier des experts en conflit. , Anne-Claire Haury (Mines Paristech/INSERM/Institut Curie)
- Oct 16 2009, 11h00 : Log-periodogram regression on non-Fourier frequencies sets. , Mohamed Boutahar (GREQAM, Université de Marseille-Luminy).
- Oct 09 2009, 11h00 : Sélection de modèles pour la classification non supervisée. , Jean-Patrick Baudry (Université de Paris-Sud)
- Jun 12 2009, 11h00 : Variations and Hurst index estimation for a Rosenblatt process using longer filters. , Frederi Viens (Purdue University, USA)
- Jun 05 2009, 11h00 : Estimation de densité avec des tailles de fenêtres locales : quelques résultats théoriques et des applications possibles. , Catherine Aaron (Université de Clermont-Ferrand)
- Apr 10 2009, 11h00 : Limit theorems for multiple sums of random variables. , Oleg Klesov (University Universität Paderborn, Allemagne and National Technical University of Ukraine)
- Apr 03 2009, 11h00 : Ratio of Generalized Hill’s estimator and its asymptotic normality theory. , Aliou Diop (Université de Saint-Louis, Sénégal)
- Mar 27 2009, 11h00 : Random attractors for stochastic Navier-Stokes equations in some unbounded domains. , Zdzislaw Brzezniak (University of York, UK)
- Mar 20 2009, 11h00 : On the stochastic Landau-Lifshitz’ Equation , Zdzislaw Brzezniak (University of York, UK)
- Feb 27 2009, 11h00 : Un point de vue statistique pour la régularisation de problèmes inverses mal posées et sa connexion avec les méthodes à noyaux. , Anna Karina Firmin (Université Paris X)
- Feb 06 2009, 11h00 : Une extension de l’ACP : les modèles auto-associatifs , Serge Iovleff (Université Lille I)
- Jan 16 2009, 11h00 : Modèles de Markov cachés en météorologie , Pierre Ailliot (Université de Brest)
- Jan 09 2009, 11h00 : Sur l’estimation fonctionnelle par le temps d’occupation , Boris Labrador (L.S.T.A., Université P. et M. Curie)
- Dec 19 2008, 11h00 : Biomarker discovery in MALDI-TOF serum protein profiles using discrete wavelet transformation , Theodore Alexandrov (Université de Breme, Allemagne)
- Oct 31 2008, 11h00 : Joint distribution of the sum and maximum of iid exponential random variables , Anna Panorska (University of Nevada, Reno, USA)




